MSc Thesis
If you build a computationally expensive simulation (of entire economies, climate systems, brains, disease spread, galaxies, text), and it has a number of hyperparameters which you need to tune (interest rates, number of synaptic connections per neuron, vaccination rates, the Hubble constant \(H_0\), number of attention heads), how do you do this?
The volume of your parameter space will grow exponentially with every hyperparameter. Say you want to test at least 10 values for each hyperparameter, across 10 parameters. If you want to explore every combination, that’s immediately \( 10^{10} \) (10 billion)!
On top of this, if one run of your simulation takes 100 seconds (which seems modest), the total runtime will be \( 10^{10} * 100 \) seconds, or, in other words, 31,710 years!
Of course, we might be able to distribute these runs across compute nodes, having access to \( 10^6 \) nodes would reduce the runtime to around 12 days. But, this would be, in most situations, prohibitively expensive.
Can we be smarter about how we explore this parameter space? Do we need all \( 10^{10} \) samples, or can we get an acceptable loss value with fewer?
This is the game Bayesian Optimisation plays, and this is what I chose to write my MSc thesis on, in the context of expensive, high-dimensional macro-economic simulation models. In particular, a flavour of simulations known as agent-based modelling (ABM), which is typically described in this agent-environment lingo, but I like to just think of it as little computer people/animals/bugs running around a computer world, bumping into things and each other, buying stuff, eating stuff, running away from and towards each other (in sometimes beautiful fashion).
I was particularly interested in how we could use Bayesian Optimisation to efficiently calibrate expensive macro-economic ABMs, which often had dozens of hyperparameters.
Within the thesis, I:
- Set up my notational mathematical world
- Filled this with a few toy macro-economic ABMs

- Pinned down some different SOTA calibration schemes
- Used them on the toy models in question

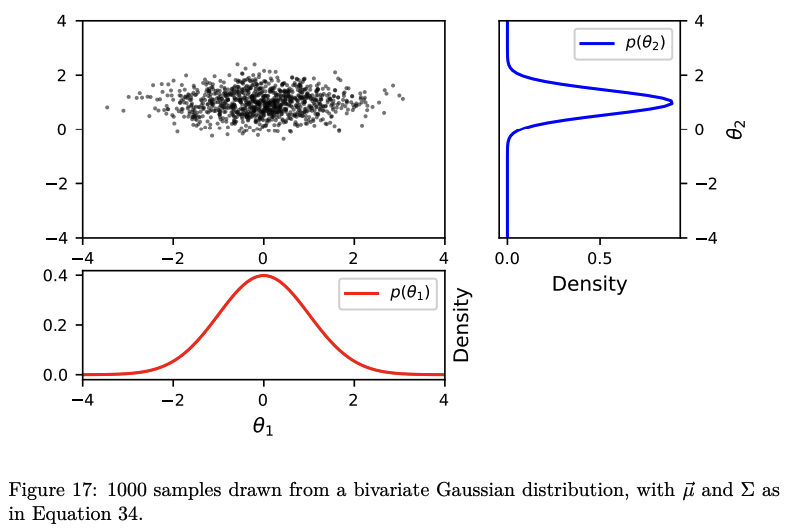
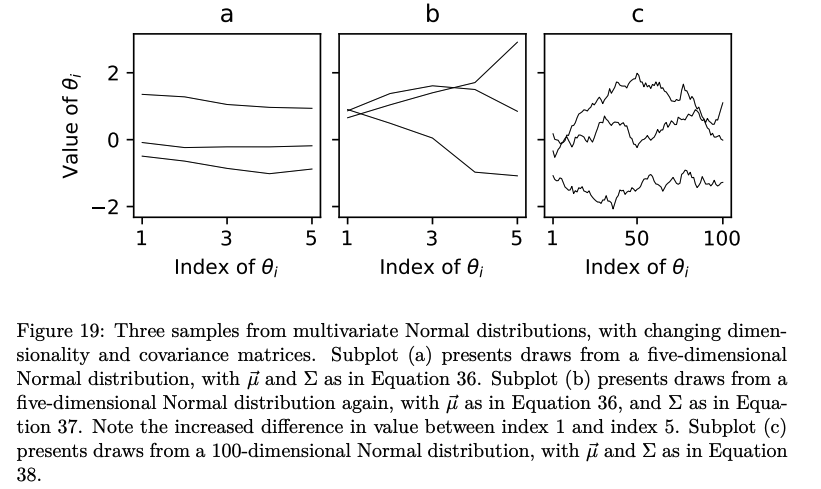
- Then, starting from the humble Gaussian, moving through multivariate Normal distributions and into covariance matrices, I build up an explanation of Gaussian Processes.
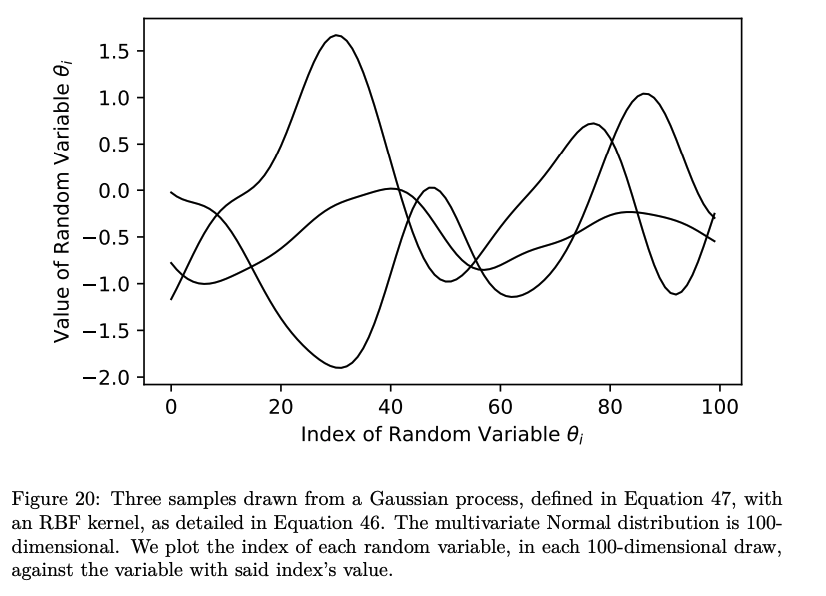
- We layer on the magic of conditioning and acquisition functions, before applying the now fully-cooked Bayesian Optimisation calibration schemes to our toy ABMs.

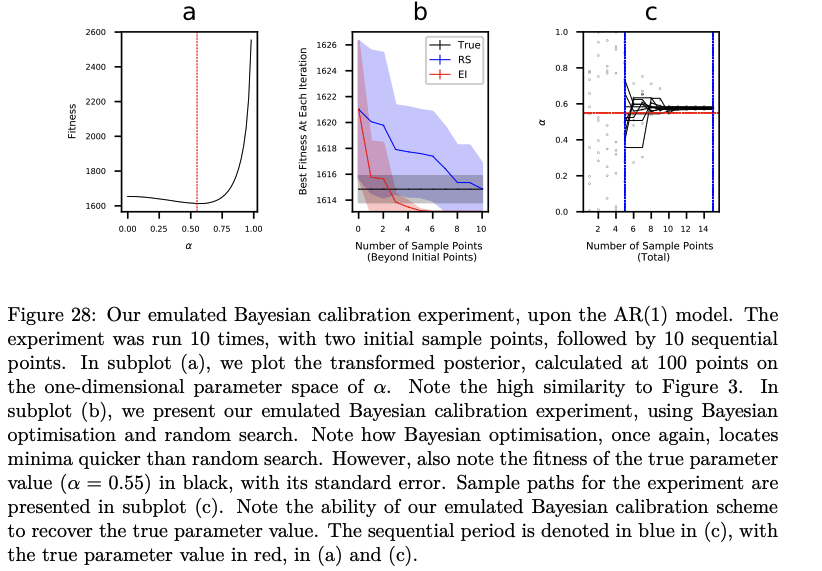
- I then discuss my main (attempted) innovation: in the most complex macro-economic ABMs, a subset of the hyperparameters are typically responsible for most of the variance.
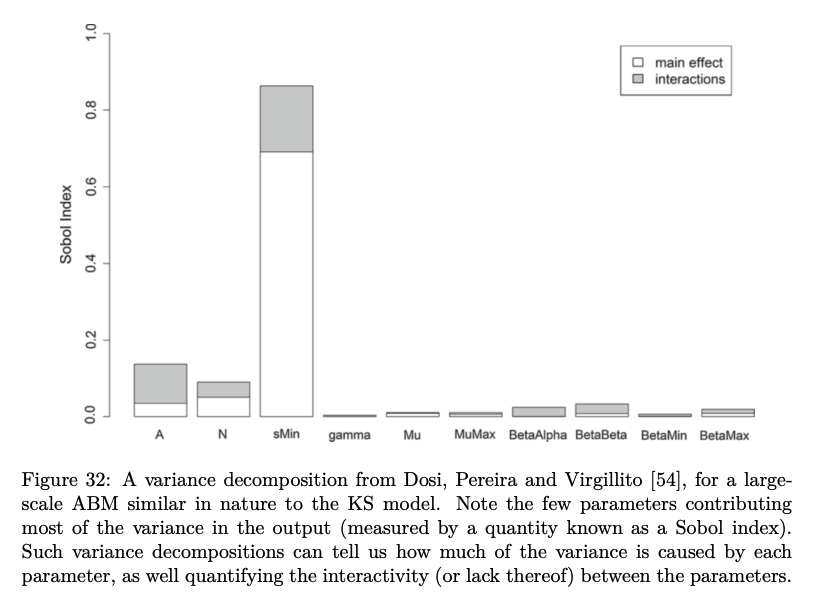
This is a sub-field of high-dimensional Bayesian Optimisation, where various schemes are cooked up to project the entire space to one of lower dimensionality, and conduct the Bayesian Optimisation there, before projecting back up. I adapted some SOTA literature on macro-economic ABM calibration to use one of these methods, tried to combine it with some SOTA NeurIPS literature on the above (re-implementing it in BOTorch), with mixed results:
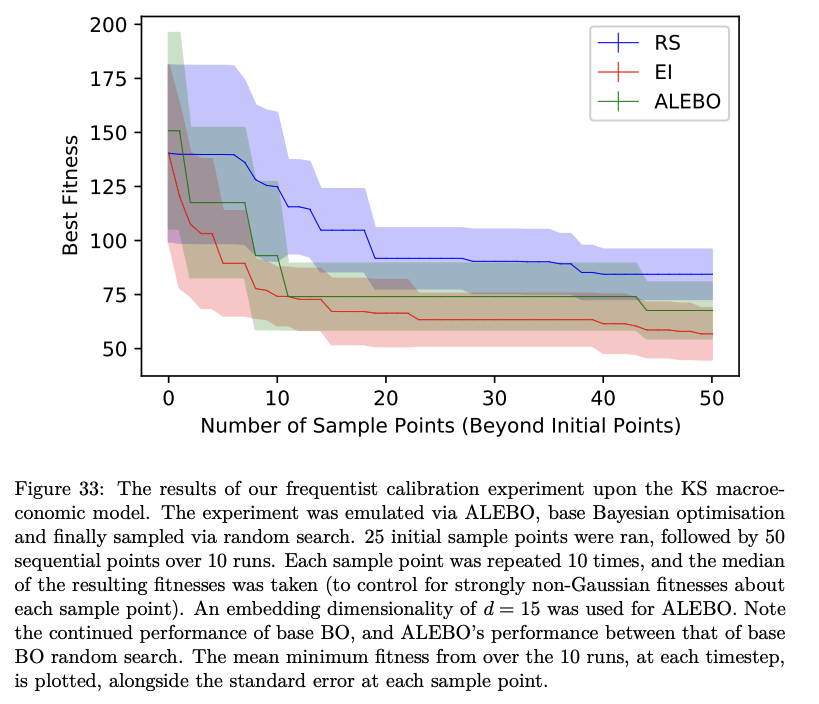
All in all, a project that I really loved doing, which delivered a document that I sometimes look back on with great fondness and pride.